• 二叉树
  • 满二叉树
  • 完全二叉树
  • BST(二插搜索树)
  • AVL(平衡二叉树)
  • B-树(平衡多路查找树)
  • B+树
  • KD树
  • KDB树
  • BKD树

二叉树、BST(二插搜索树)、AVL(平衡二叉树)、B-树(平衡多路查找树)、B+树、KD树、KDB树、BKD树

二叉树

子树最多只有两棵的树

前序遍历：根结点 —> 左子树 —> 右子树

中序遍历：左子树 —> 根结点 —> 右子树

后序遍历：左子树 —> 右子树 —> 根结点

满二叉树

每层节点是满的树

完全二叉树

n个节点和满二叉树一致，即满二叉树缺失最后一行的最后几个节点

BST(二插搜索树)

目的是为了提高搜索性能，采用二分思想，每个节点的值大于其任意左侧子节点的值，小于其任意右节点的值，具体实现时为了效率一般会使用二分思想，使左右子树节点数量尽量平均

AVL(平衡二叉树)

在符合二插搜索树的前提下，满足任何节点的两个子树的高度最大差为1，在插入或者删除数据时，可以通过旋转使树重新平衡

LL旋转

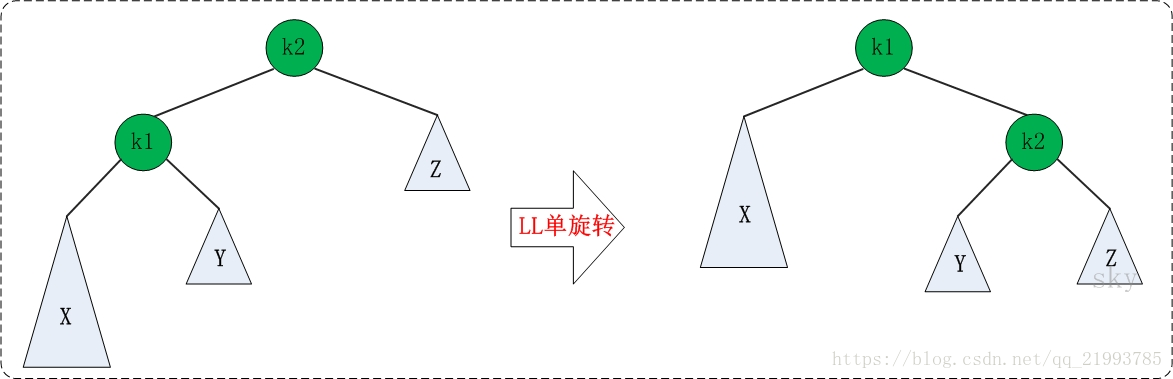
RR旋转

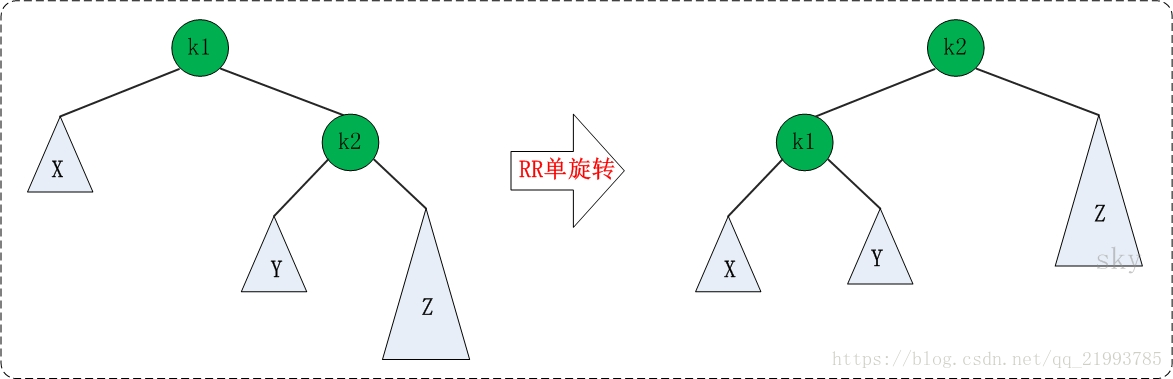
LR旋转

RL旋转

B-树(平衡多路查找树)

1. 每个节点最多有m个孩子

2. 除了根节点和叶子节点外，其它每个节点至少有Ceil(m/2)个孩子

3. 若根节点不是叶子节点，则至少有2个孩子

4. 所有叶子节点都在同一层，且不包含其它关键字信息

5. 每个非终端节点包含n个关键字信息（P0,P1,…Pn, k1,…kn）

6. 关键字的个数n满足：ceil(m/2)-1 <= n <= m-1

7. ki(i=1,…n)为关键字，且关键字升序排序

8. Pi(i=1,…n)为指向子树根节点的指针。P(i-1)指向的子树的所有节点关键字均小于ki，但都大于k(i-1)

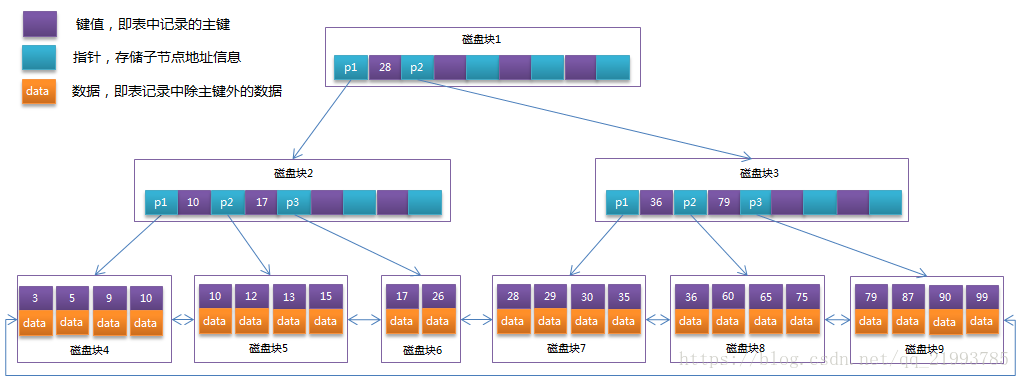
下面是一个3阶的B-树

B+树

B+Tree是在B-Tree基础上的一种优化，数据量较大时会导致B-Tree深度较大

B+Tree相对于B-Tree有几点不同：

1. 非叶子节点只存储键值信息。
2. 所有叶子节点之间都有一个链指针。
3. 数据记录都存放在叶子节点中。

KD树

空间树的一种，使用的还是二分思想，只不过节点数据是多维的，重点是如何划分数据

顺序遍历法：即对于点（x1, x2, x3, x4 ….），第一次按x1的维度来切分，第二次按照x2的维度来切分，切到最后一个维度之后又回到x1的维度

KDB树

KD树和B+树结合体，但是可以预见的是存在大量空间浪费

BKD树

BKD树由多个可修改的KDB树构成，是一个完全二叉树，叶子节点存储的和KDB树一模一样

BKD树不会被修改，添加新数据时，在内存中有一个完全二叉树作为buffer，size=M。外部存储（硬盘）里保存的第i棵树，要么是空的，要么是2^i * M 这么大

1、每次插入的时候，如果buffer没满，那就直接在内存里插入

2、如果满了，找到第一个空的树，将前面所有做merge

这样最多只会有M的空间浪费